멈추지 않고 끈질기게
[알고리즘] 팰린드롬 찾기 - Manacher's Algorithm 본문
※ 해당 포스팅은 개인의 공부 정리용 글입니다. 틀린 내용이 있다면 추후 수정될 수 있습니다.
※ 해당 포스팅은 하기 출처들을 참조하였습니다.
- https://m.blog.naver.com/jqkt15/222108415284
[알고리즘] Manacher’s Algorithm - 마나커(마나허) 알고리즘
어떤 문자열에서 팰린드롬의 개수와 위치를 찾는 알고리즘인 "Manacher's Algorithm"에 ...
blog.naver.com
- https://small-stepping.tistory.com/987
마나커(Manacher) 알고리즘
1. 마나커 알고리즘(Manacher's Algorithm)이란?어떤 문자열에서 팰린드롬의 개수와 위치를 찾는 알고리즘이다. 팰린드롬이란?팰린드롬(회문, Palindrome)은 전체 문자열을 뒤집었을 때 원래 상태와 같은
small-stepping.tistory.com
1. 팰린드롬 찾기
팰린드롬(palindrome)이란 순서를 뒤집어도 똑같은 문장 혹은 단어를 의미하며, 우리말로는 회문(回文)이라고 합니다. 예를 들면 'eye', '기러기', '다시 합창합시다' 등이 팰린드롬에 속합니다. 코딩 테스트에서도 종종 등장하는 주제로, 주어진 문자열의 부분문자열 중 가장 긴 팰린드롬을 찾는 등의 문제가 주어집니다.
하나의 문자열이 팰린드롬인지 아닌지를 검사하는 것은 큰 어려움이 없습니다. 문자열의 시작과 끝에서부터 한칸씩 이동하며 검사하면, 문자열의 길이가 n이라고 할 때 n / 2번 반복하여 체크할 수 있습니다. 다만 위에서 언급한 것처럼 모든 부분문자열 중 가장 긴 팰린드롬을 찾는 것은 단순하게 이중 반복문을 돌렸다간 약 O(n ^ 2)의 시간복잡도를 가지게 됩니다. 이와 같은 문제를 O(n)의 시간복잡도로 해결하는 방법이 마나커 알고리즘(Manacher's Algorithm)입니다.
2. 마나커 알고리즘
마나커 알고리즘은 반복문을 돌며 해당 위치의 문자를 중심으로 한 팰린드롬의 최대 길이를 검사합니다. 일반적인 방법과 다른 점은, 이전에 검사한 데이터를 기반으로 현재 위치의 최소 팰린드롬 길이를 갱신하고 시작한다는 점입니다. 이전 데이터를 활용한다는 점에서 일종의 동적 계획법(Dynamic Programming)이라고 볼 수 있습니다.

예를 들어 "asdfdsd"라는 문자열이 주어진다면, 맨 왼쪽 a부터 마지막 d까지 순회하며 해당 문자를 중심으로 한 최대 팰린드롬의 길이를 검사한 후 저장하고, 이 중 가장 큰 값을 반환하는 방식입니다. 여기서 가장 중요한 부분은 'i번째 문자열의 검사를 어디부터 시작할 것인가' 입니다. 이를 위해 마나커 알고리즘에서는 현재까지 검사한 팰린드롬 중 가장 긴 팰린드롬의 중심점과 오른쪽 끝 위치를 저장해둡니다.
현재까지 검사한 가장 긴 팰린드롬의 중심점을 c, 오른쪽 끝 위치를 r, 그리고 i번째 문자를 중심으로 하는 최대 팰린드롬 길이를 DP[i]라고 하겠습니다. c는 이전 검사 과정에서 갱신한 값이므로, i보다는 항상 왼쪽에 있습니다. 그리고 r이 i보다 오른쪽에 있다면 다음과 같은 3가지 경우가 발생할 수 있습니다.
1) 현재 문자를 중심으로 한 팰린드롬이 검증된 가장 긴 팰린드롬 안에 속함
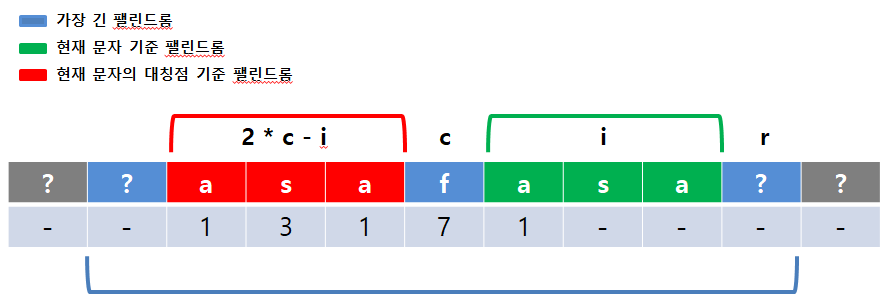
해당 경우, i와 i의 c를 기준으로 한 대칭점(2 * c - i)이 동일한 길이의 팰린드롬일 수 밖에 없습니다. 왜냐하면 c를 기준으로 한 팰린드롬 안에 두 팰린드롬이 속해 있으므로, 만약 한쪽의 팰린드롬의 길이가 다르다면 c를 기준으로 팰린드롬이 성립할 수가 없기 때문입니다. 따라서 DP[i] = DP[2 * c - i]가 성립합니다.
2) 현재 문자를 중심으로 한 팰린드롬이 검증된 가장 긴 팰린드롬의 끝과 겹침
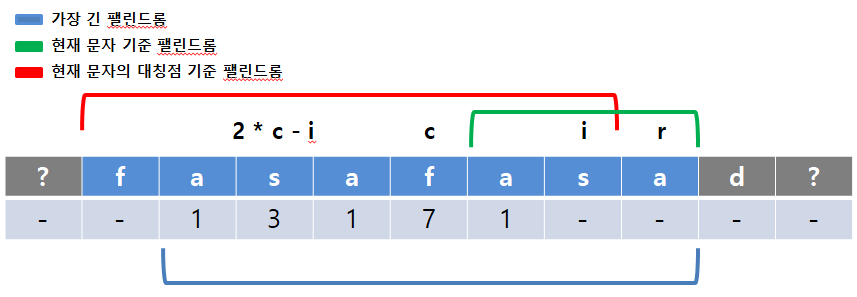
해당 경우에는 위의 예시처럼 i와 i의 대칭점의 팰린드롬의 길이가 같지 않을 수 않습니다. 다만 이 경우, 상황 전제에서 이미 현재 문자 기준 팰린드롬이 r과 겹친다고 가정하고 있으므로 r까지는 팰린드롬임이 보장된다고 할 수 있습니다. 즉, r- i만큼은 팰린드롬임이 보장되므로 DP[i] = r - i로 시작할 수 있습니다.
3) 현재 문자를 중심으로 한 팰린드롬이 검증된 가장 긴 팰린드롬 영역을 벗어남
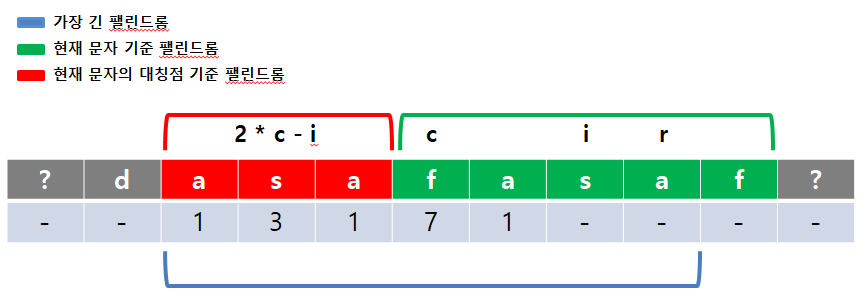
해당 경우에는 i 기준 팰린드롬이 어디까지 이어질지는 예상할 수 없으나, 2)와 비슷하게 r 너머까지 팰린드롬이라고 가정하고 있으므로 r - i 만큼 팰린드롬임이 보장됩니다. 즉, DP[i] = r - i로 시작할 수 있습니다.
또한 위의 3가지 케이스는 r < i 임을 전제로 하고 있습니다. i >= r 인 경우, 검증된 영역을 벗어나므로 DP[i] = 0으로 시작해야 합니다. 그렇다면 r < i 인 경우, 위의 3가지 케이스 중 어디에 속하는지 어떻게 검사해야 할까요? 1)의 경우 DP[2 * c - i]이고 나머지 경우 r - i로 초기화해야 하는데, 1번 케이스의 경우 i 기준 팰린드롬이 반드시 r보다 좌측에서 끝나야하기 때문에 DP[2 * c - i] < r - i 가 성립합니다. 또한 2, 3번 케이스의 경우 i 기준 팰린드롬이 최소 r과 겹치거나 넘어가는 경우이므로, DP[2 * c - i] >= r - i 가 성립합니다. 이를 유심히 살펴보면, DP[2 * c - i] 와 r - i 중 상황에 맞는 값이 작거나 같다는 점을 확인할 수 있습니다. 따라서 두 값 중 작은 값을 선택하면 됩니다.
(참고로 아래에 설명할 임시 문자를 삽입한 이후 기준으로 계산해야 해당 식이 정확하게 성립합니다.)
추가로 해당 방식은 한 문자를 기준으로 양쪽으로 뻗어나가면서 검사하기 때문에, 홀수 크기의 팰린드롬만 측정할 수 있습니다. 이를 해결하려면 문자열의 각 문자 앞뒤로 임시 문자를 삽입한 후에 검사를 시작해야 합니다.

위와 같이 임시 문자(#)를 삽입한 후 해당 알고리즘을 사용하면 짝수 팰린드롬에도 대응할 수 있게 됩니다. 문자열의 길이가 2배로 늘어났지만, 대칭 검사 후 DP[i] 값을 1씩만 늘리면 자연스럽게 길이는 맞게 됩니다. 위 사진은 문자열 "assaf"에 임시 문자를 삽입해서 검사한 결과로, 두 개의 s 사이의 임시 문자를 기준으로 4번의 대칭이 성립하여 최대 팰린드롬 길이 4가 나온 것을 확인할 수 있습니다.
3. 코드 예시
C++로 작성한 마나커 알고리즘의 예시 코드입니다.
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int longest_palindrome(const string& s)
{
// 임시 문자 삽입하여 연장(짝수 팰린드롬 대응)
string extended = "#";
for(const char& c : s)
{
extended += c;
extended += "#";
}
int len = extended.size();
vector<int> DP(len); // 각 문자를 중심으로 한 팰린드롬의 길이
int c = 0; // 현재까지 검사한 팰린드롬 중 가장 긴 것의 중심점
int r = 0; // 현재까지 검사한 팰린드롬 중 가장 긴 것의 오른쪽 끝
for(int i = 0; i < len; ++i)
{
// DP[i] 초기화
// i > r 이라면 검증된 팰린드롬을 벗어났음을 의미 => DP[i] = 0
// 이외의 경우, 다음과 같은 3가지 케이스가 존재
// 1) 현재 문자 기준 팰린드롬이 검증된 가장 긴 팰린드롬 안에 존재
// - 현재 문자의 c를 기준으로 한 대칭점(2 * c - i)과 동일한 길이만큼 팰린드롬임이 보장됨
// - 따라서 DP[i] = DP[2 * c - i]
// 2) 현재 문자 기준 팰린드롬이 검증된 가장 긴 팰린드롬과 겹치는 경우
// - 검증된 가장 긴 팰린드롬까지는 팰린드롬임이 보장됨
// - 따라서 DP[i] = r - i
// 3) 현재 문자 기준 팰린드롬이 검증된 가장 긴 팰린드롬을 넘어가는 경우
// - 검증된 가장 긴 팰린드롬까지는 팰린드롬임이 보장됨
// - 따라서 DP[i] = r - i
//
// 1)의 경우 DP[2 * c - i] < r - i (검증된 가장 긴 팰린드롬을 넘어가지 않아야 하므로)
// 2), 3)의 경우 r - i <= DP[2 * c - i] (검증된 가장 긴 팰린드롬과 겹치거나 넘어가야 하므로)
// => DP[2 * c - i] 와 r - i 중 작은 값으로 초기화
DP[i] = i > r ? 0 : min(DP[2 * c - i], r - i);
// 문자열 범위를 벗어나지 않고, 양쪽 끝 문자가 같다면 DP[i] 증가
while (i + DP[i] + 1 < len && i - DP[i] - 1 >= 0
&& extended[i + DP[i] + 1] == extended[i - DP[i] - 1])
++DP[i];
// 현재 문자 기준 팰린드롬의 오른쪽 끝이 r을 넘어갔다면 r, c 갱신
if(i + DP[i] > r)
{
r = i + DP[i];
c = i;
}
}
// 검사한 모든 팰린드롬 길이 중 가장 큰 값을 반환
return *max_element(DP.begin(), DP.end());
}
int main()
{
cout << "문자열을 입력하세요: ";
string s;
cin >> s;
cout << "가장 긴 팰린드롬의 길이: " << longest_palindrome(s) << "\n";
}

이론적인 부분이 이해하기 쉽지 않은데 비해, 코드 자체는 굉장히 단순한 편입니다. 짝수 팰린드롬도 찾을 수 있도록 임시 문자를 삽입한 문자열을 만들고, 해당 문자열의 길이만큼 반복문을 돌며 DP[i] 초기화 및 팰린드롬 연장 가능 여부를 검사하고 가장 긴 팰린드롬을 갱신하면 됩니다. for문 안에 while이 들어가는 이중 반복문 구조라서 O(n ^ 2)가 아닌가 싶지만, 긴 팰린드롬을 찾고 나면 이후의 DP[i]가 높은 값으로 시작하므로 일반적인 방법보다 검사 횟수가 훨씬 줄어들게 됩니다. 범용적으로 사용되는 알고리즘은 아니지만, 팰린드롬을 찾는데 있어서는 굉장히 효율적이므로 기억해두고 가야겠습니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 소수 관련(에라토스테네스의 체, 골드바흐 추측) (0) | 2024.09.12 |
|---|---|
| [알고리즘] 백 트래킹(back-tracking) (0) | 2024.09.08 |
| [알고리즘] 이분법(Bisection method) (0) | 2023.10.18 |
| [알고리즘] 동적 계획법(Dynamic Programming) (0) | 2023.09.21 |
| [알고리즘] 그리디 알고리즘(Greedy Algorithm) (0) | 2023.09.03 |




