멈추지 않고 끈질기게
[알고리즘] 동적 계획법(Dynamic Programming) 본문
※ 해당 포스팅은 개인의 공부 정리용 글입니다. 틀린 내용이 있다면 추후 수정될 수 있습니다.
※ 해당 포스팅은 하기 출처들을 참조하였습니다.
- 존 캐리, 코딩 테스트를 위한 자료구조와 알고리즘 with C++, 도서출판 길벗, 2022
이번 포스팅에서는 동적 계획법(Dynamic Programming)에 대해 알아보도록 하겠습니다.
1. 동적 계획법이란
동적 계획법(Dynamic Programming, 이하 DP)이란 문제를 해결하기 위해 해당 문제를 여러개의 부분 문제로 나누고, 그 부분 문제의 해답을 이용하여 전체 문제를 해결하는 방식을 말합니다. A*와 같이 특정 기능에 특화된 알고리즘은 아니고, 일종의 방법론에 속합니다. 동적 계획법을 적용하려면 문제가 다음과 같은 특성을 만족해야 합니다.
- 1) 중복되는 부분 문제(overlapping subproblem)
전체 문제를 분할하는 과정에서 같은 부분 문제가 반복적으로 나타나는 특성
- 2) 최적 부분 구조(optimal substructure)
전체 문제의 해답이 부분 문제의 해답으로 구성되는 특성
대표적인 예시로 n번째 피보나치 수열을 구하는 예시를 들 수 있습니다. 피보나치 수열은 알다시피 다음과 같은 특성을 지닙니다(F(n) = n번째 피보나치 수열 값).
- 1) 0번째 값은 0, 1번째 값은 1
- 2) n > 1일 경우, F(n) = F(n - 1) + F(n - 2)
그리고 해당 특징을 그대로 코드로 옮기면 n번째 피보나치 수열 값을 구하는 함수를 재귀함수 형태로 쉽게 구현할 수 있습니다.
public long Fibonacci(int count)
{
if (count < 2)
return count;
return Pibonachi(count - 1) + Pibonachi(count - 2);
}다만 해당 함수를 통해 n번째 값을 구할 경우, 계산 과정에 중복이 엄청 많이 발생합니다. 예를 들어 Fibonacci(5)의 경우 Fibonacci(4) + Fibonacci(3)이고, Fibonacci(4)에서 다시 Fibonacci(3) + Fibonacci(2)를 계산합니다. 이 때 이미 계산한 Fibonacci(3)을 다시 계산하게 되고, n이 커질수록 이러한 중복 계산이 엄청나게 많아지게 됩니다. 현재 제 자가 PC로 Fibonacci(60)을 실행했더니 4분이 넘도록 계산이 끝나지 않았습니다.
이런 문제점을 피하고 계산 효율을 높이기 위해 지난 연산 결과를 다음 연산에 재활용하자는 것이 동적 계획법의 기본 발상입니다. 피보나치 수열의 경우, 다음과 같이 배열을 선언하고 이전 계산값을 저장했다가 사용하는 방식으로 효율을 크게 올릴 수 있습니다.
public long Fibonacci2(int count)
{
long[] arr = new long[count];
arr[0] = 0;
arr[1] = 1;
for (int i = 2; i < count; i++)
arr[i] = arr[i - 1] + arr[i - 2];
return arr[count - 1];
}위 코드에서는 중복 계산이 발생하지 않고, 이전 계산값을 활용하여 O(n)의 시간복잡도로 빠르게 값을 구할 수 있습니다. Fibonacci2(60)의 경우, 동일 PC에서 1초도 안되어 계산이 끝나는 모습을 확인할 수 있었습니다.
동적 계획법은 접근 방식에 따라 메모이제이션(Memoization)과 타뷸레이션(Tabulation)으로 나뉩니다. 메모이제이션은 하향식 접근 방식으로 재귀 함수와 동일하게 접근하되 계산 결과를 저장해두고, 이후에 이미 계산한 값은 저장소에서 꺼내 사용하는 방식입니다. 타뷸레이션은 상향식 접근 방식으로, 기저 조건에서부터 시작하여 원하는 결과를 찾을때까지 올라가는 방식입니다. 위의 Fibonacci2() 함수가 이에 속하며, F(n) = F(n - 1) + F(n - 2)라는 관계식을 통해 0번째부터 차례대로 올라가며 계산해나갑니다.
2. 코드 예제(부분집합의 합, 배낭 문제)
동적 계획법을 적용할 수 있는 대표적인 문제로는 부분집합의 합 문제가 있습니다. 이 문제는 한마디로, 양의 정수로 이루어진 집합의 부분집합 중 원소의 합이 x와 같은 부분집합이 존재하는가? 를 구하는 문제입니다. 얼핏 보면 단순한 문제같지만, 가능한 모든 부분집합의 경우의 수를 다 구하려면 원소의 개수에 따라 연산량이 기하급수적으로 늘어납니다.
부분집합의 합 문제의 경우 1) 부분집합이 더 작은 부분집합의 집합으로 구성되므로 최적 부분 구조 속성을 만족, 2)부분집합이 중복되어 나타날 수 있으므로 중복되는 부분 문제 속성을 만족하므로 동적 계획법을 적용할 수 있습니다. 다음은 부분집합의 합 문제를 동적 계획법으로 해결하는 코드 예시입니다.
// 랜덤 원소 집합 생성 및 SubSet() 실행
class Program
{
static void Main(string[] args)
{
Random r = new Random();
int[] arr = new int[5];
for (int i = 0; i < 5; i++)
arr[i] = r.Next(1, 100);
Console.WriteLine("전체 집합의 원소들:");
foreach(var num in arr)
Console.Write(num + " ");
Console.WriteLine("\n");
DP.SubSet(arr);
}
}// 모든 부분집합의 합을 구하는 함수
public class DP
{
public static void SubSet(int[] arr)
{
int maxSum = 0;
for (int i = 0; i < arr.Length; i++)
maxSum += arr[i];
bool[,] DP = new bool[arr.Length + 1, maxSum + 1];
for (int i = 0; i < arr.Length; i++)
DP[i, 0] = true;
for (int i = 1; i <= arr.Length; i++)
{
for (int sum = 1; sum <= maxSum; sum++)
{
if (sum < arr[i - 1])
DP[i, sum] = DP[i - 1, sum];
else
DP[i, sum] = DP[i - 1, sum] || DP[i - 1, sum - arr[i - 1]];
}
}
Console.WriteLine("가능한 부분집합의 합:");
for (int sum = 0; sum <= maxSum; sum++)
{
if (DP[arr.Length, sum])
Console.Write(sum + " ");
}
Console.WriteLine();
}
}
메인 함수에서는 원소 5개짜리 배열에 1~99 범위의 무작위 숫자를 저장하고, 해당 배열을 매개변수로 SubSet() 함수를 호출했습니다. SubSet() 함수는 부분집합의 합을 구하는 함수로, 동적 계획법을 이용합니다.
우선 bool 타입의 2차원 배열 DP를 선언합니다. 사이즈는 (부분집합 합을 구할 배열의 원소 수 + 1) * (배열의 모든 원소의 합 + 1)로 생성하고, 다음과 같은 규칙을 이용하여 값을 채웁니다.
- 1) x라는 값을 n-1번째 원소까지 이용해 만들 수 있다면, n번째 원소에서도 만들 수 있다고 판단한다.
- 2) n번째 원소 값을 a라고 할 때 x - a라는 값을 n-1번째 원소까지 이용해 만들 수 있다면,
n번째 원소에서도 만들 수 있다고 판단한다.
예를 들어 DP[2, 10] 이 true라면 두번째 원소까지 사용해서 합계 10을 만들 수 있다는 뜻이고, 그렇다면 DP[3, 10]도 true로 설정합니다. 또한 3번째 원소가 5라면, 여기에 5를 더해서 15를 만들 수 있다는 뜻이므로 DP[3, 15]도 true로 설정합니다. 즉, DP[n, sum]이 true라면 n번째 원소까지 사용했을 때 부분집합의 합이 sum이 될 수 있다는 뜻입니다. 상기 코드에서는 이중 for문 안에서 이 과정을 진행하며, 완료 후 1차원 인덱스가 집합의 크기, 2차원 인덱스가 n일 때 true라면(DP[집합의 크기, n] == true) 부분집합의 합으로 n을 만들 수 있다는 뜻입니다. 사진 1이 상기 예제의 실행 결과로, 가능한 모든 부분집합의 합을 보여주고 있습니다.
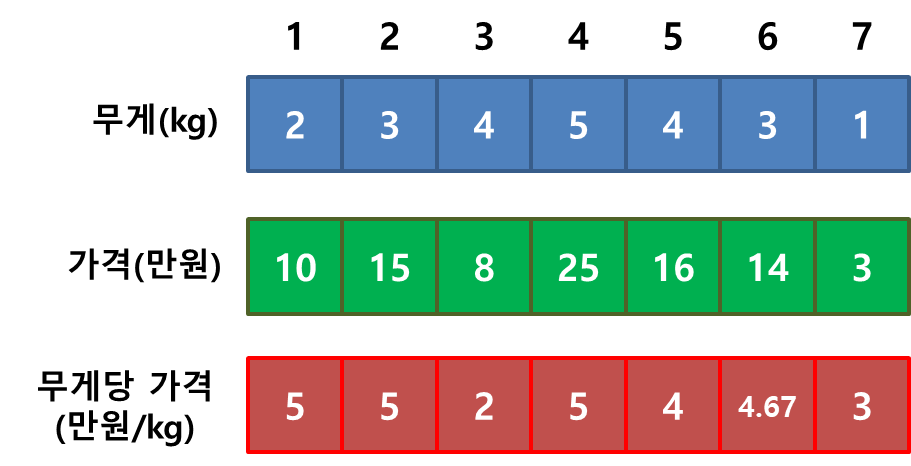
또한 그리디 알고리즘 포스팅에서 언급한 배낭 문제의 경우 그리디 알고리즘으로는 가능한 최고 가격을 구할 수 없었지만, 동적 계획법을 통해 구할 수 있습니다.
다음 코드는 배낭 문제를 동적 계획법을 통해 구하는 코드 예시입니다.
public static void BackPack(int[] prices, int[] weights, int wLimit)
{
// int형 2차원 배열 선언([상품, 무게])
// 원소의 값은 누적된 상품 가격을 저장
int[,] DP = new int[prices.Length + 1, wLimit + 1];
for (int i = 1; i <= prices.Length; i++)
{
int curPrice = prices[i - 1];
int curWeight = weights[i - 1];
// 1) w가 현재 조사할 상품의 무게보다 낮다면 이전 단계의 값으로 저장
// 2) 1번 외의 경우, '이전 단계의 같은 무게 값(DP[i - 1, w])'과
// '이전 단계에서 현재 상품 무게보다 적은 무게의 값(DP[i - 1, w - curWeight])
// + 현재 상품의 가격(curPrice)를 합친 값' 중 더 높은 값을 저장
for (int w = 1; w <= wLimit; w++)
{
if (w < curWeight)
DP[i, w] = DP[i - 1, w];
else
DP[i, w] = Math.Max(DP[i - 1, w], DP[i - 1, w - curWeight] + curPrice);
}
}
// 배열에서 마지막 단계의 무게 제한에 저장된 값(DP[prices.Length, wLimit])이 가능한 최대 상품 가격
Console.WriteLine($"가방에 담을 수 있는 최대 가격: {DP[prices.Length, wLimit]}");
}
구현 내용은 부분집합의 합 문제와 거의 비슷하나, DP 배열을 bool 대신 int형으로 선언했습니다. 2차원 인덱스를 무게로 설정하고, 원소값은 누적된 상품 가격을 저장하도록 했습니다. 이중 for문 안에서 마찬가지로 DP 배열을 채워나가는데, 이때 다음과 같은 규칙으로 저장합니다.
- 1) 현재 탐색하는 무게(w)가 현재 상품의 무게보다 낮다면 이전 단계의 값으로 저장
- 2) 1번 외의 경우,
- 이전 단계의 같은 무게의 가격(DP[i - 1, w])
- 이전 단계에서 현재 상품 무게보다 적은 무게의 가격(DP[i - 1, w - curWeight]) + 현재 상품의 가격(curPrice)을 합친 값
둘 중 더 높은 값을 저장
2번 규칙에 의해 같은 무게의 더 높은 가격 조합이 나온다면 값이 갱신되고, 더 낮은 값이 나올땐 무시하므로 반복문이 끝난 후에 마지막 단계의 최대 무게에 저장된 값(DP[상품의 수, 최대 무게])이 배낭에 담을 수 있는 가장 비싼 가격이 됩니다. 사진 2는 그리디 알고리즘 포스팅에서 예를 든 배낭 문제(그림 1)를 해당 함수로 풀어본 결과로, 그리디 알고리즘으로는 찾지 못했던 최대값 29를 찾은 모습을 보여주고 있습니다.
3. 장점과 단점
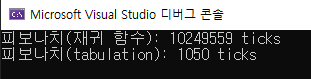
동적 계획법은 일반적인 재귀 함수를 통한 문제 풀이에 비해 시간 효율이 굉장히 높은 모습을 보여줍니다. 맨 처음 피보나치 수열의 예시에서 보았듯이 재귀적으로 구현했을 때 발생하는 중복 계산을 피하고, 이전 계산 결과를 활용하기 때문입니다. 사진 3는 피보나치 수열 40번째 수를 재귀 함수 방식과 타뷸레이션 방식으로 구할 때 걸린 시간을 Stopwatch 클래스를 통해 측정한 것으로, 약 10,000배의 차이가 난 것을 확인할 수 있습니다.
특히 타뷸레이션의 경우 부분집합의 합 문제에서 볼 수 있듯이 부분문제들의 해답을 모두 저장한 테이블이 만들어지므로, 특정 값 외에도 다양한 값을 확인하고 싶을 때 유용합니다(ex. n번째 원소까지의 모든 부분집합의 합).
다만 동적 계획법은 구현 난이도가 높다는 단점이 있습니다. 동적 계획법을 사용하려면 해당 문제에서 각 부분문제간의 관계를 식으로 표현할 수 있어야 하므로, 해당 문제에 대한 깊은 이해도를 요구합니다. 사실 위의 코드 예제들은 참고한 책에 설명이 있었지만, 코드를 몇번이나 지웠다 새로 써보고 실행 중에 값을 추적해보면서 겨우 제대로 이해할 수 있었습니다. 물론 이 단점은 본인의 능력에 달린 것이므로, 문제에 따라 동적 계획법을 적절하게 사용할 수 있도록 공부해야겠습니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 팰린드롬 찾기 - Manacher's Algorithm (0) | 2024.08.19 |
|---|---|
| [알고리즘] 이분법(Bisection method) (0) | 2023.10.18 |
| [알고리즘] 그리디 알고리즘(Greedy Algorithm) (0) | 2023.09.03 |
| [알고리즘] A* 알고리즘 (0) | 2023.08.24 |
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2023.08.22 |




