멈추지 않고 끈질기게
[알고리즘] 백 트래킹(back-tracking) 본문
※ 해당 포스팅은 개인의 공부 정리용 글입니다. 틀린 내용이 있다면 추후 수정될 수 있습니다.
※ 해당 포스팅은 하기 출처들을 참조하였습니다.
- https://edder773.tistory.com/75
[파이썬] 탐색 알고리즘 정리 - 백트래킹
백트래킹 (*Notion AI의 설명) 백트래킹(Backtracking)은 해결책을 구하기 위해 모든 가능성을 시도해보는 것이 아니라, 해결책에 대한 후보군을 구성하고 그 후보군이 문제의 조건을 만족하는지 여부
edder773.tistory.com
[백트래킹] 백트래킹의 설명과 간단한 예제풀이
백트래킹(Backtracking) 1. 백트래킹이란? 백트래킹은 알고리즘 기법 중 하나로, 재귀적으로 문제를 하나씩 풀어가면서 현재 재귀를 통해 확인 중인 노드(상태)가 제한된 조건에 위배되는지 판단하
youngdroidstudy.tistory.com
1. 백 트래킹(back-tracking)
백 트래킹이란 조건을 만족하는 한 계속 검사해 나가다, 조건에 부합하지 않는 순간 탐색을 취소하고 이전 단계로 돌아온 뒤 탐색을 이어나가는 알고리즘을 말합니다. 설명에서 짐작할 수 있듯이 DFS 기반의 알고리즘으로, 재귀 함수나 스택을 통해 구현할 수 있습니다.
백 트래킹 알고리즘의 대략적인 의사 코드를 작성하자면 다음과 같습니다.
void back_tracking(int count)
{
if(현재 상태가 마지막까지 도달한 경우)
정답 카운팅
return;
for(가능한 모든 경우에 대해)
{
조건을 만족하는지 검사
if(조건을 만족하는 경우)
{
상태값 저장
back_tracking(count + 1);
상태값 원복
}
}
}
우선 재귀적으로 실행할 함수를 선언합니다. 해당 함수에는 조건을 검사하기 위한 매개변수와 현재 상태를 체크하기 위한 매개변수가 필요합니다. 현재 상태가 마지막까지 도달한 경우, 가능한 경우의 수를 발견한 것이므로 정답으로 카운팅합니다. 그 외의 경우에는 가능한 모든 경우에 대해 반복문을 돌며 검사하고, 조건을 만족하는 경우 재귀적으로 호출합니다. 이 때, DFS처럼 함수 호출 이전에 상태값을 저장하고 호출 후에 원복시킴으로서 검사가 끝난 케이스에 영향을 받지 않도록 합니다. 조건을 만족하는 경우가 없다면 현재 호출 스택 이후로 돌아가므로 해당 상태 이후에 대한 탐색을 중단하게 되는데, 이를 가지치기(pruning)이라 합니다. 따라서 백 트래킹은 DFS와 비슷하지만, 가지치기를 통해 도중에 탐색 범위를 줄여가면서 진행하므로 문제에 따라 효율적인 접근 방법이 됩니다.
2. 코드 예시(N-Queen 문제)
백 트래킹을 활용하여 풀 수 있는 문제에는 대표적으로 N-Queen 문제가 있습니다. N-Queen 문제란, N x N 사이즈의 체스판에 N개의 퀸을 놓을 수 있는 경우의 수를 계산하는 문제입니다. 퀸은 체스에서 가장 강력한 기물로, 퀸이 놓인 수평, 수직 방향 및 대각선 방향 전부를 공격할 수 있습니다. 즉, N개의 퀸을 수평, 수직, 대각선 방향 전부 겹치지 않게 놓아야 합니다. N = 4인 경우 다음 그림과 같은 2가지 경우의 수가 존재합니다.

해당 문제는 다음과 같은 백 트래킹을 활용한 코드를 통해 계산할 수 있습니다.
#include <iostream>
#include <vector>
using namespace std;
void back_tracking(int N, int count, vector<int>& queen, int& ans)
{
if(count == N)
{
++ans;
return;
}
for(int i = 0; i < N; ++i)
{
bool able = true;
// 놓을 수 있는 위치인지 검사
for (int j = 0; j < count; ++j)
{
if (queen[j] == i || count - j == abs(queen[j] - i))
{
able = false;
break;
}
}
if (false == able) continue;
queen[count] = i;
back_tracking(N, count + 1, queen, ans);
queen[count] = 0;
}
}
int main()
{
int N = 10; // 임의의 N 선언
int answer = 0;
vector<int> queen(N, 0);
back_tracking(N, 0, queen, answer);
cout << answer;
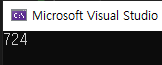
}
우선 백 트래킹을 위해 구하고자 하는 N의 값과 현재 퀸의 갯수, 퀸의 배치 정보를 담을 벡터와 정답을 담을 변수를 매개변수로 받는 함수를 선언합니다. 함수 내부는 현재 배치한 퀸의 개수만큼 배치 정보를 체크하며 count번째 행에 퀸을 배치할 수 있는지 검사하고, 배치할 수 있다면 배치 정보에 기록한 후 count를 1 늘려서 재귀적으로 실행합니다. 이 때 실행 후에는 배치 정보를 이전 상태로 원복시킵니다. 마지막으로 count가 N과 같다면 N개의 퀸의 배치가 가능한 경우에 다다른 것이므로 정답을 카운팅합니다.
여기서 핵심은 퀸의 배치 정보를 1차원 벡터에 담는다는 점입니다. 우선 퀸을 하나라도 배치하면 해당 행에는 더 이상 퀸을 배치할 수 없으므로, 맨 위의 행에서부터 퀸을 배치하면서 내려온다고 생각하면 해당 행의 전체 정보는 어차피 필요하지 않습니다. 1차원 벡터의 i번째 원소에 몇 번째 열에 퀸을 배치했는지만 저장하면, 1차원 벡터로도 수직, 수평 방향으로 배치 가능 여부를 검사할 수 있습니다. 마지막으로 대각선 방향의 검사가 남아있는데, 이 또한 열 정보만으로 해결 가능합니다. 체스판에서 대각선 위치에 있는 경우 |행의 차이| == |열의 차이|가 성립하므로, 수평 방향과 함께 검사하면 배치 가능 여부를 전부 검사할 수 있습니다(코드 예시의 20번째 라인).
3. 결론
백 트래킹 알고리즘은 DFS에 기반하여 원리 자체가 그렇게 어렵진 않지만, 실제로 활용하려면 조건 검사 및 상태 원복 로직을 고심해서 짤 필요가 있습니다. 앞서 소개한 N-Queen 문제의 경우, 퀸을 놓은 배치 정보를 체스판이라고 단순히 2차원 배열로 저장하면 검사 과정의 비용이 너무 커져서 시간 효율성이 크게 떨어지게 됩니다. 하지만 N-Queen 외에도 1부터 N 까지의 자연수 중 M개를 고르는 문제 등에서 활용하기 좋은 알고리즘이므로 문제를 좀 더 풀어보며 학습해야겠습니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 플로이드-워셜(Floid-Warshall) 알고리즘 (0) | 2024.09.24 |
|---|---|
| [알고리즘] 소수 관련(에라토스테네스의 체, 골드바흐 추측) (0) | 2024.09.12 |
| [알고리즘] 팰린드롬 찾기 - Manacher's Algorithm (0) | 2024.08.19 |
| [알고리즘] 이분법(Bisection method) (0) | 2023.10.18 |
| [알고리즘] 동적 계획법(Dynamic Programming) (0) | 2023.09.21 |




