멈추지 않고 끈질기게
[기타][메모용] 행렬의 변환 본문
※ 해당 포스팅은 개인의 공부 정리용 글입니다. 틀린 내용이 있다면 추후 수정될 수 있습니다.
※ 해당 포스팅은 하기 출처들을 참조하였습니다.
- 프랭크 D.루나, DirectX 12를 이용한 3D 게임 프로그래밍 입문(류광 옮김), 한빛미디어, 2021
1. 선형 변환, 행렬의 표현
- 3차원 벡터를 입력받아 3차원 벡터를 출력하는 함수가 다음 조건을 만족할 경우,
3차원 벡터에 대한 선형 변환(linear transformation)이라고 함
- u와 v는 임의의 3차원 벡터, k는 스칼라 값

- 함수가 상기 두 조건을 모두 만족한다면(선형 변환이라면), 다음 성질이 성립함

- 모든 3차원 벡터는 단위 벡터 i(1, 0, 0), j(0, 1, 0), k(0, 0, 1)로 다음과 같이 표현할 수 있음

- 선형변환 함수는 그림 2에서 살펴본 성질과 그림 3의 벡터 표현을 통해 스칼라값과 단위 벡터에 대한 선형 변환으로
표현할 수 있음
- 이 형태는 곧 벡터와 행렬의 곱셈이므로, 선형변환을 행렬의 형태로 표현할 수 있음
=> 선형변환의 행렬 표현(matrix representation)

2. 비례 변환, 회전 변환
- 비례 변환(scaling transformation): x축, y축, z축 값에 각각 스칼라 값을 곱하는 선형 변환
- 비례 변환 식은 다음과 같이 정의됨

- 비례 변환은 선형 변환이므로 행렬로 표현 가능
- 물체를 표현하는 좌표값에 각각 비례 행렬을 곱할 경우, 물체의 크기를 바꾸는 효과가 있음
- 그림 7은 최솟점(-2, -2, 0), 최댓점(2, 2, 0)으로 정의되는 정사각형에 비례 행렬을 곱하여 크기를 변경한 예시


- 회전 변환(rotation transformation): 벡터 n을 축으로 θ만큼 회전하는 회전 공식은 벡터의 내적과 외적을 통해 정의됨
- 회전 변환 또한 선형변환의 일종이므로 벡터로 표현 가능 => 회전 행렬(R)
- 회전축 n이 x축, y축, z축일 경우 회전 행렬이 아주 간단해짐


3. 동차좌표와 아핀변환
- 벡터는 본래 방향과 크기만을 표현한 것이므로, 이동 변환의 영향을 받으면 안됨
- 동차 좌표(homogeneous coordinate):3차원 벡터에 w라는 값을 추가하여 점과 벡터를 구분하도록 만든 것
(x, y, z, 0) => 벡터, (x, y, z, 1) => 점
- 3차원 좌표계를 4x4 배열의 형태로 표현하는 이유
- 아핀변환: 선형변환에 이동벡터를 더한 것
- 벡터 u의 좌표와 선형 변환의 행렬 표현의 곱에 이동벡터를 더하는 식으로 표현 가능
- w = 1인 동차좌표를 도입하면 아핀변환을 4x4 행렬로 간단하게 표현할 수 있음
(w = 0일 경우, 이동벡터 b값은 모두 무시되는 부분에 주목)
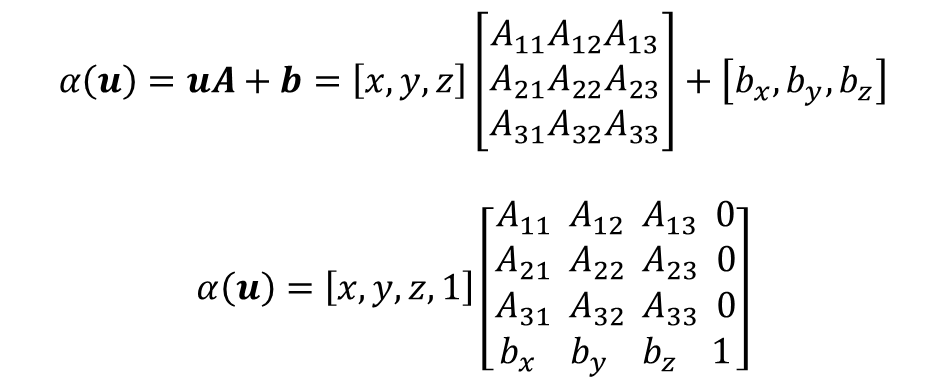
- 이동변환은 상기 아핀변환의 행렬 표현에서 행렬 A에 해당하는 부분을 단위행렬로 치환하여 표현 가능
- 회전변환 또한 행렬 A에 해당하는 부분에 넣어 동차좌표에 적용할 수 있음

- 유니티의 Transform 또한 데이터를 동차좌표를 적용한 4x4 배열 형태로 저장(Matrix4x4)
- 이동변환 및 회전변환의 행렬 표현을 곱하여 변환을 적용할 수 있음
- ex) 회전 행렬을 통한 오브젝트 회전 예시
// 3차원 큐브에 적용
public class TransformTest : MonoBehaviour
{
void Start()
{
// 30도를 라디안 단위로 변환
float radian_30 = 30 * Mathf.Deg2Rad;
// y축 기준 30도 회전변환의 행렬 표현
Matrix4x4 rotMatrix = new Matrix4x4() {
m00 = Mathf.Cos(radian_30), m01 = 0, m02 = -Mathf.Sin(radian_30), m03 = 0,
m10 = 0, m11 = 1, m12 = 0, m13 = 0,
m20 = Mathf.Sin(radian_30), m21 = 0, m22 = Mathf.Cos(radian_30), m23 = 0,
m30 = 0, m31 = 0, m32 = 0, m33 = 1
};
// 현재 오브젝트의 월드좌표계 행렬
Matrix4x4 curMatrix = transform.localToWorldMatrix;
// y축 기준 30도 회전
curMatrix *= rotMatrix;
// 회전값 적용
transform.SetPositionAndRotation(curMatrix.GetPosition(), curMatrix.rotation);
}
}
4. 강체 변환, 변환의 합성
- 강체(rigid body) 변환: 물체의 형태에 영향을 미치지 않는 변환(회전, 이동 등)
- 강체 변환은 회전 변환과 이동 벡터의 합으로 표현할 수 있음 => 아핀 변환
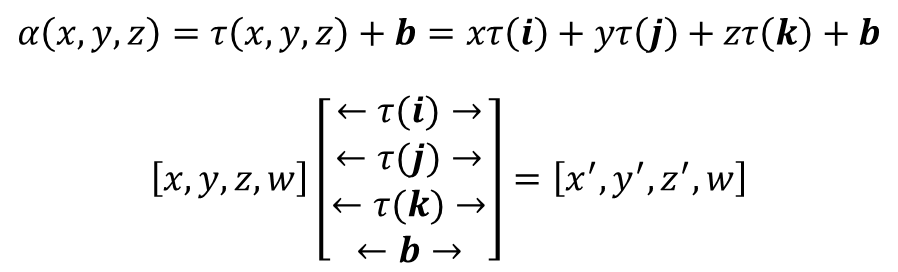
- 비례 변환, 회전 변환, 이동 변환 등 선형 변환들은 행렬의 형태로 표현 가능함
- 변환의 적용 => 정점(w=1인 벡터)과 변환 행렬의 곱셈
- 행렬의 곱셈은 결합법칙 적용 가능 => 연속된 변환을 하나의 행렬로 합성할 수 있음
- ex) 비례변환, 회전변환, 이동 변환을 순차적으로 적용할 경우,
회전행렬 S와 회전행렬 R과 이동행렬 T를 순차적으로 곱한 하나의 변환행렬로 합성 가능(SRT)

- 유니티에서도 Matrix4x4 구조체에서 이동행렬 및 회전행렬을 쉽게 구할 수 있는 기능 제공
- 이동행렬과 회전행렬을 곱하여 합성한 뒤 현재 트랜스폼의 행렬에 곱하고, 이를 토대로 포지션 및 회전을 갱신하면
한꺼번에 적용됨을 확인 가능
// 3차원 큐브에 적용
public class TransformTest : MonoBehaviour
{
void Start()
{
Matrix4x4 curMatrix = transform.localToWorldMatrix;
// x축으로 2만큼, y축으로 4만큼, z축으로 5만큼 이동
Matrix4x4 moveMatrix = Matrix4x4.Translate(new Vector3(2, 4, 5));
// x축, y축, z축 기준 30도 회전
Matrix4x4 rotMatrix = Matrix4x4.Rotate(Quaternion.Euler(Vector3.one * 30));
// 변환 합성
Matrix4x4 combMatrix = moveMatrix * rotMatrix;
curMatrix *= combMatrix;
transform.SetPositionAndRotation(curMatrix.GetPosition(), curMatrix.rotation);
}
}
'기타' 카테고리의 다른 글
| [기타][메모용] 코테에서 자주 나오는 실수 (0) | 2024.04.11 |
|---|---|
| [기타][메모용] 길찾기 관련 (0) | 2023.08.06 |
| [Photon][저장용] IP 변경 시 설정 (0) | 2023.06.03 |
| [기타][저장용] 어셈블리 언어 (0) | 2023.02.28 |
| [기타] 모바일 디바이스의 특징 (0) | 2023.02.14 |


