멈추지 않고 끈질기게
[알고리즘] 너비 우선 순회(BFS) / 깊이 우선 순회(DFS) 본문
※ 해당 포스팅은 개인의 공부 정리용 글입니다. 틀린 내용이 있다면 추후 수정될 수 있습니다.
※ 해당 포스팅은 하기 출처들을 참조하였습니다.
- 존 캐리, 코딩 테스트를 위한 자료구조와 알고리즘 with C++, 도서출판 길벗, 2022
이번 포스팅에서는 그래프 순회 알고리즘의 기본이 되는 너비 우선 순회(BFS)와 깊이 우선 순회(DFS)에 대해 알아보겠습니다.
1. 너비 우선 순회(BFS, Breadth-First Search)
너비 우선 순회(이하 BFS)는 현재 정점과 연결된 모든 정점을 먼저 방문하고, 이 후 방문한 정점으로 넘어가서 해당 과정을 반복하는 방식입니다. 예를 들기 위해 다음과 같은 그래프가 있다고 가정하겠습니다.
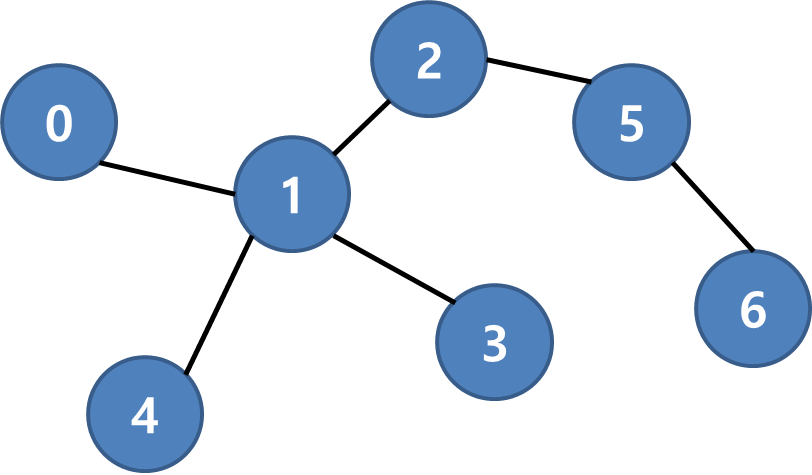
상기 그래프의 0번에서 시작하여 BFS를 통해 모든 정점을 순환할 경우, 우선 0번 정점에 연결된 1번 정점을 방문합니다. 이후 1번 정점에 연결된 모든 정점(2, 3, 4)을 방문한 뒤, 추가로 연결된 정점이 남아있는 2번으로 이동하여 해당 과정을 반복합니다. 즉, 0 > 1 > 2 > 3 > 4 > 5 > 6 의 순서로 방문하게 됩니다.
다음은 C# 코드로 작성한 그림 1의 그래프를 BFS를 통해 순환하는 예시입니다.
// 그래프 표현
static int[,] graph =
{
{ 0, 1, 0, 0, 0, 0, 0 },
{ 1, 0, 1, 1, 1, 0, 0 },
{ 0, 1, 0, 0, 0, 1, 0 },
{ 0, 1, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 1, 0, 0, 0, 1 },
{ 0, 0, 0, 0, 0, 1, 0 }
};
// 방문 체크용 배열
static bool[] visited = new bool[7];
static void Main(string[] args)
{
Bfs(0);
}
static void Bfs(int start)
{
// 방문 예정을 큐에 저장
Queue<int> que = new Queue<int>();
que.Enqueue(start);
while (que.Count > 0)
{
int cur = que.Dequeue();
visited[cur] = true;
Console.WriteLine($"{cur}번 정점 방문");
for (int next = 0; next < 7; next++)
{
// 연결되지 않았거나 이미 방문했다면 스킵
if (graph[cur, next] == 0 || visited[next])
continue;
// 방문 예정에 추가
que.Enqueue(next);
}
}
}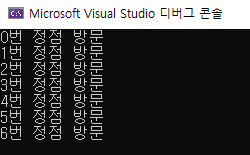
graph는 그림 1의 그래프를 2차원 배열 형태로 표현한 것으로 이어지지 않은 경우 0, 이어진 경우 1로 표현하였습니다. visited는 각 정점의 방문 여부를 저장하는 배열입니다.
BFS는 Queue를 통해 간단하게 구현할 수 있습니다. 큐를 선언한 뒤 시작지점을 저장하고, 반복문 안에서는 현재 위치를 큐에서 출력하여 받아온 뒤 해당 정점을 방문했을 때 필요한 내용을 실행합니다. 추가로 반복문을 돌며 그래프에서 연결되지 않았거나 이미 방문한 정점이라면 스킵하고, 아직 방문하지 않은 연결된 정점은 큐에 추가하여 예약합니다. 해당 로직을 반복하면 큐의 선입선출 특성상 방문한 정점에 연결된 모든 정점들을 우선적으로 방문하여 자동적으로 BFS 방식이 됩니다.
2. 깊이 우선 순회(DFS, Depth-First Search)
깊이 우선 순회(이하 DFS)는 현재 정점과 연결된 정점 중 하나를 방문한 뒤, 방문한 정점에서 다시 연결된 정점으로 이동합니다. 더이상 연결된 정점이 없을때까지 반복한 뒤, 아직 방문하지 않은 정점에 연결된 정점까지 회귀하고 앞의 방식을 반복합니다. 예를 들기 위해 그림 1을 다시 가져왔습니다.

상기 그래프의 0번에서 시작하여 DFS를 통해 모든 정점을 순환할 경우, 우선 0번 정점에 연결된 1번 정점을 방문합니다. 다음으로 1번 정점에 연결된 정점 중 하나를 방문하는데, 2번을 먼저 방문할 경우 2번과 연결된 5번, 5번과 연결된 6번을 먼저 방문합니다. 더이상 연결된 정점이 없으므로 다시 회귀하여 1번으로 돌아온 뒤, 남은 3번과 4번을 방문하여, 0 > 1 > 2 > 5 > 6 > 3 > 4 의 순서로 방문하게 됩니다.
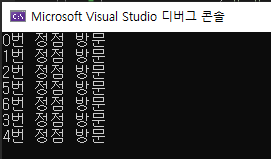
다음은 C# 코드로 작성한 그림 1의 그래프를 DFS를 통해 순환하는 예시입니다.
// 그래프 표현
static int[,] graph =
{
{ 0, 1, 0, 0, 0, 0, 0 },
{ 1, 0, 1, 1, 1, 0, 0 },
{ 0, 1, 0, 0, 0, 1, 0 },
{ 0, 1, 0, 0, 0, 0, 0 },
{ 0, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 1, 0, 0, 0, 1 },
{ 0, 0, 0, 0, 0, 1, 0 }
};
// 방문 체크용 배열
static bool[] visited = new bool[7];
static void Main(string[] args)
{
Dfs(0);
}
// 재귀함수 구현
static void Dfs(int cur)
{
visited[cur] = true;
Console.WriteLine($"{cur}번 정점 방문");
for (int next = 0; next < 7; next++)
{
// 연결되지 않았거나 이미 방문했다면 스킵
if (graph[cur, next] == 0 || visited[next])
continue;
// 방문할 지점을 재귀적으로 호출
Dfs(next);
}
}
(graph 및 visited는 BFS 예시와 동일합니다.)
DFS는 재귀함수를 통해 간단하게 구현할 수 있습니다. 반복문을 돌며 아직 방문하지 않은 이어진 정점을 찾은 뒤, 해당 점점을 방문하는 DFS 함수를 재귀적으로 호출함으로서 자동으로 연결된 정점을 우선적으로 방문하게 됩니다. 위 예제의 결과를 보면 0 > 1 > 2 > 5 > 6 > 3 > 4 의 순서로 DFS 방식으로 순회하였음을 확인할 수 있습니다.
static void Dfs(int start)
{
// 방문 예정을 스택에 저장
Stack<int> stk = new Stack<int>();
stk.Push(start);
while (stk.Count > 0)
{
int cur = stk.Pop();
visited[cur] = true;
Console.WriteLine($"{cur}번 정점 방문");
for (int next = 0; next < 7; next++)
{
// 연결되지 않았거나 이미 방문했다면 스킵
if (graph[cur, next] == 0 || visited[next])
continue;
// 방문 예정에 추가
stk.Push(next);
}
}
}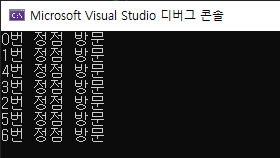
추가로 DFS의 경우 BFS 예제에서 방문 예정을 저장하는 자료구조만 Queue에서 Stack으로 바꾸어 구현할 수도 있습니다. 스택의 후입선출 특성상 자동으로 저장한 정점들 중 마지막 정점에 방문하고, 이를 반복하면 연결된 정점을 계속 방문하게 되기 때문입니다. 다만 스택 사용 시 마지막으로 방문한 정점부터 파고들기 때문에, 방문 순서가 재귀함수로 구현했을 때와 달리 0 > 1 > 4 > 3 > 2 > 5 > 6 로 순서가 변경되었음을 알 수 있습니다.
3. BFS, DFS의 한계
BFS와 DFS는 그래프의 모든 정점을 비교적 단순한 로직으로 순회할 수 있다는 장점이 있지만, 정점 간의 거리(간선)에 가중치가 없는 그래프에만 사용할 수 있다는 한계가 있습니다. 위에서 알아보았듯이 해당 알고리즘은 간선의 가중치를 고려하지 않으므로, 사용할 수 있는 대상이 제한됩니다.
간선에 가중치가 존재하는 그래프에 적용할 수 있는 알고리즘으로는 다익스트라(Dijkstra) 알고리즘이 있습니다. 이동할 때마다 각 간선의 가중치를 정점에 저장, 혹은 더 낮은 값으로 갱신하여 특정 정점까지의 최단 경로를 찾아내는데 사용할 수 있는 알고리즘입니다. 다익스트라 알고리즘에 대해서는 다음 포스팅에서 다루도록 하겠습니다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘(Greedy Algorithm) (0) | 2023.09.03 |
|---|---|
| [알고리즘] A* 알고리즘 (0) | 2023.08.24 |
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (0) | 2023.08.22 |
| [알고리즘] 우선순위 큐(Priority Queue) (0) | 2023.08.11 |
| [알고리즘] 트리(Tree) (0) | 2023.08.10 |




